- arrow_back Home
- keyboard_arrow_right Highlights
How to Model Extraction Economies
HighlightsJournal 48 Phillip Black April 21
The answer to extraction shooters lies in system design. By creating a model, we can derive implications that help guide key design decisions and frame challenges in a quantifiable way. A model also lays plain some of the variables that shape the experience of extractions. There’s a reason Marathon’s design director mentioned a target survival rate of 50% (the percentage of players who successfully extract). This single variable has enormous implications for how players experience progression.
Hint: it’s the casino dummy.
Similar to social casino, the genre creates “runs” where players can extract wealth or resources.
Each successful run means more wealth and greater stakes. And like social casino, the genre has developed player “hedges” but turned them into progression vectors. For instance, players can ‘stash’ income or utilize ‘insurance’ slots, which enable them to protect specific resources in the event of a failed extraction. Players “buy” down cooldown time by earning cash in-game, opening the possibility of strong out-of-game economy activities.
These “persistence” elements boost survival rates through their relative effects, and setting targets against these is the most crucial decision an extraction game makes. The higher the power score ceiling, the higher the long-run win rates for a given player throughout a season. Critically, PvE elements provide predictable encounters and stable resource gains, making player survival rates tunable.
Player-to-player trade is critical. Like Zynga Poker, players almost inadvertently trade with one another when they die and drop gear. Gear degradation, such as weapons losing effectiveness over multiple runs, helps control in-game economic inflation. Escape from Tarkov implemented a similar system, and the model is further discussed in “How to Solve ‘THE’ Web3 Problem: A Staircase Tax.“
Similar to the Monopoly Go model, to understand the effects, I created a simplified version of Call of Duty’s DMZ mode. I wanted my model to:
- Simulate the first 100 player runs
- Track net wealth and player level
- Show how vertical progression influences the survival rate
- Show how “insurance” and stash influence player progression
- Show how many successful consecutive runs a player will have throughout a season or timespan
- And take less than 3 hours to build!
The result is here and available for download. Eventually, we’ll produce this:
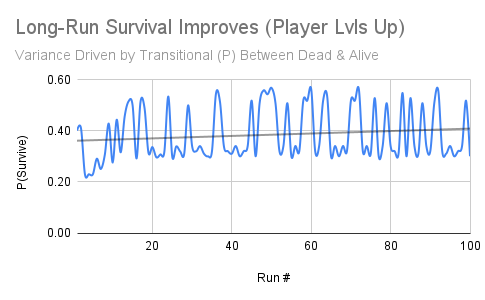
Markov Chains & the Extractor’s Dilemma
To understand the “reset” effect, I utilize simple Markov Chains, which model transitional states. To start, I create a simple matrix and start a list of runs to model.

Here, I suggest that the chance of surviving if the player last survived is 35%, while there’s a 65% chance of dying. If the player last died, it’s far more likely (80%) that the player will die again. This is an assumption, but it simply reflects a simplifying aspect of the “resetting” aspect of extraction-economies. The massive inequality between the Survive and Death conditional probabilities could be called the Extractors’ Dilemma.
Vertical Progression
However, vertical progression improves survival odds as players complete contracts and gain stat boosts or new weapons. I create a lookup table and bound the power score gain relative to a wild stab at what FPS players expect. Survival odds of consecutive survivals increase by 15 percentage points by level 20, to 50%, and the probability of surviving after a death jumps 10 percentage points.


I calculate XP values for Survival and Death, and based on the survival rate, we determine the expected XP per run. We then use a lookup table to find the player’s level. The new player level (if applicable) will influence the survival chance, which we vary based on whether the last player’s result was death or survival at each level.

There are two additional survival odd modifiers, a slot modifier and another one for streaks. The slot bonus is an additional survival chance assumption based on the particular insured slot a player enters the match with, while the streak bonus is a cheeky modeling assumption for consecutive survivals.1Together with level, they shape a long-run upward survival rate.
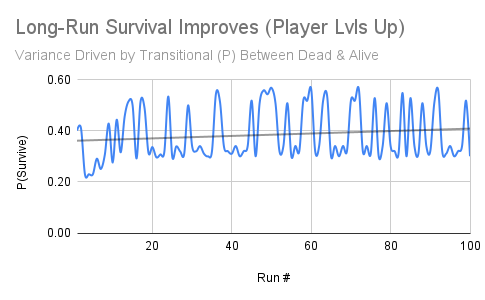
Once we have the survival rate, I simulate a single player by generating a random number, and if the survival rate exceeds it, the player survives. This is also how streaks are created: by counting consecutive wins.


Cooldown, Insurance, and Weapon Slots
The final, and most considerable part of the build, is the assumptions around cooldown, insurance, and weapon slots. Here, we assume a player unlocks an insured weapon slot at particular levels. Each slot has a specific cooldown, in minutes, during which a player cannot use the weapon; however, earning cash in a match reduces the cooldown. We also assume a player takes one weapon into the match, and the slots are ordered from best to worst (since cooldown increases for the n+1 slot, a player always wants their best weapon in slot 1). If a player does not have a weapon off cooldown, they spend cash on a weapon.2


Getting the cooldown logic right was a step-by-step process of layering on additional rules. First, there’s the rule only to use the slot if the slot ahead is on cooldown, then there’s the cash cooldown reduction, and finally, a day “reset.” This was achieved by simply setting a runs/day assumption.


Together, this finally determines the slot in which a player will enter the match equipped.

P2P, MM & More
What’s not here is player-to-player trade or matchmaking effects – introducing separate maps, or SBMM, or an Apex-style ranked point system are worth building extensions too. At the very least, our model build helps us understand the genre and consider how design inventions affect the player experience.